KMP

相关资源#

总结自b站课程#

​ 最浅显易懂的 KMP 算法讲解_哔哩哔哩_bilibili ↗

力扣题目#

KMP的的实现过程#

1.匹配过程#

在模拟 KMP 匹配过程之前，我们先建立两个概念：

前缀：对于字符串 abcxxxxefg，我们称 abc 属于 abcxxxxefg 的某个前缀。

后缀：对于字符串 abcxxxxefg，我们称 efg 属于 abcxxxxefg 的某个后缀。

首先匹配字符串时，先遍历主串，寻找可以开始与子串相匹配的地方，刚开始和普通的暴力算法没有区别，一个个匹配，直到出现无法匹配的字母

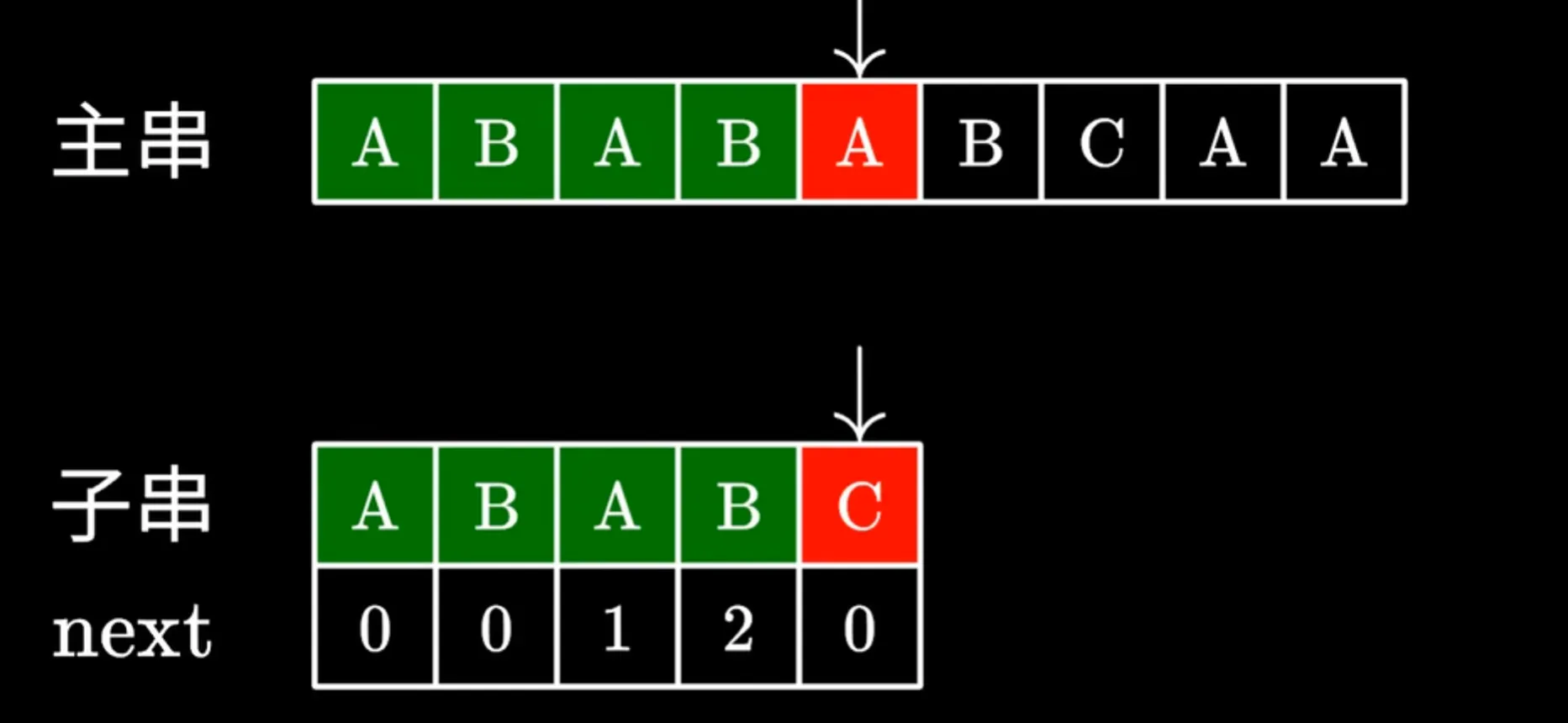
暴力算法的方法是将指针回退到开始匹配的位置的下一个字母再来一次匹配（主串指针回退到B，子串重新匹配）

而KMP对子串设置了一个next数组，当匹配出现错误时，它会保持主串中的指针不变，查询子串不匹配位置（C）的上一个字母（B）在next数组中所对应的值，这个值所代表的是子串指针重新放置的索引位置，如下图

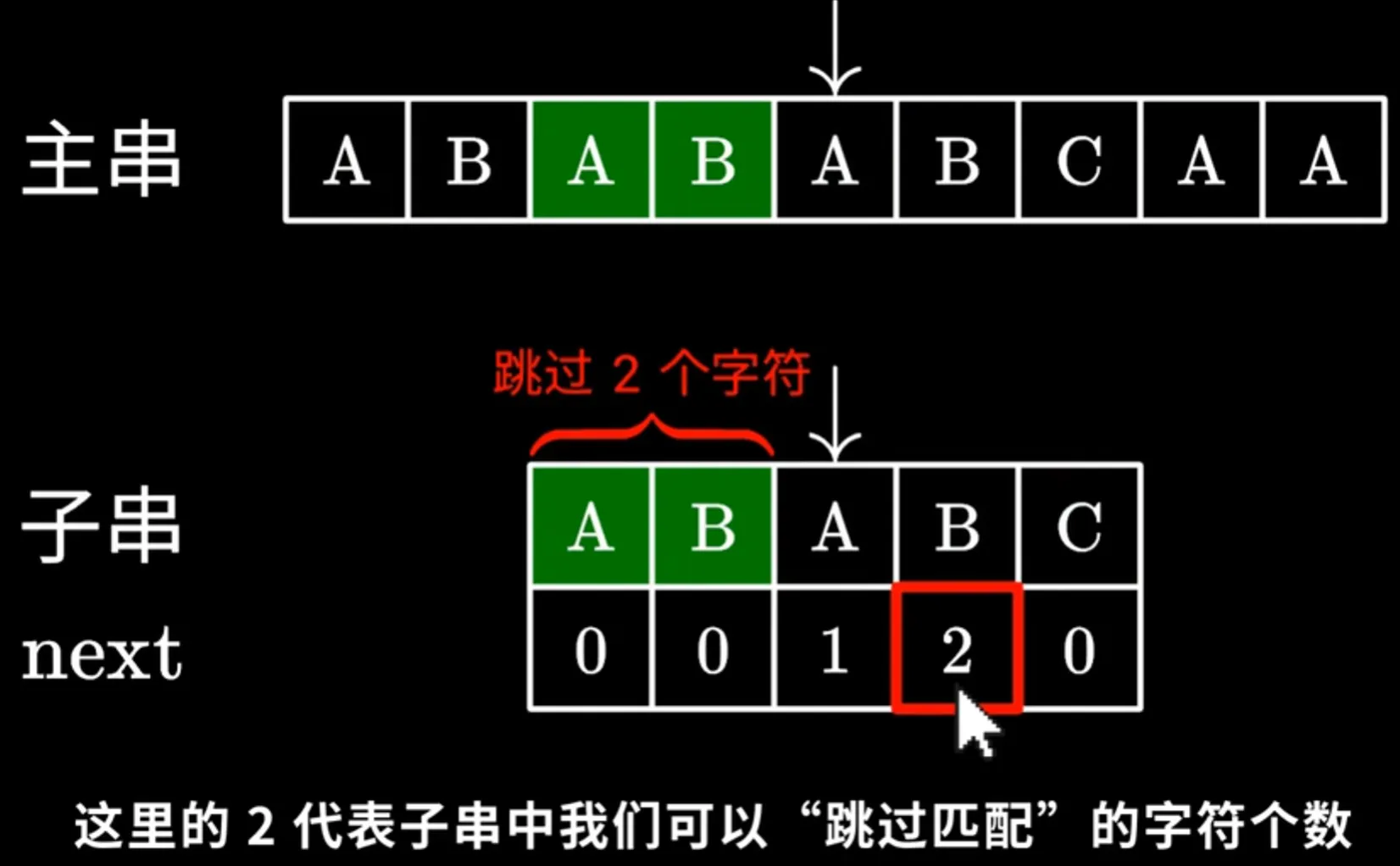
如此再继续往下匹配，如有不同重复此操作，便可实现目的

以下是代码实现：

假设主串是“sadbutsad” 字串是“sad”

string haystack = "sadbutsad";
string needle = "sad";
int len1 = haystack.size(), len2 = needle.size();

for(int i = 0, j = 0;i < len1; ++i){//i为主串的指针 j为子串的指针
	if(haystack[i] == needle[j]){//当前字符是否相同
		if(j == len2 - 1){//匹配成功
			return i - j;//返回子串在主串中的开始索引
		}
        j++;
    }else if(j != 0){//中途不匹配 查next数组操作
    	j = next[j - 1];//移动子串指针
        i--;//保持主串指针不动
    }
}

2.next数组(重点所在)#

现在 就是正式地解释一下next数组了。

next数组里记录的是从开始字符到当前字符所组成的字符串中最大的共同前后缀长度 如下图

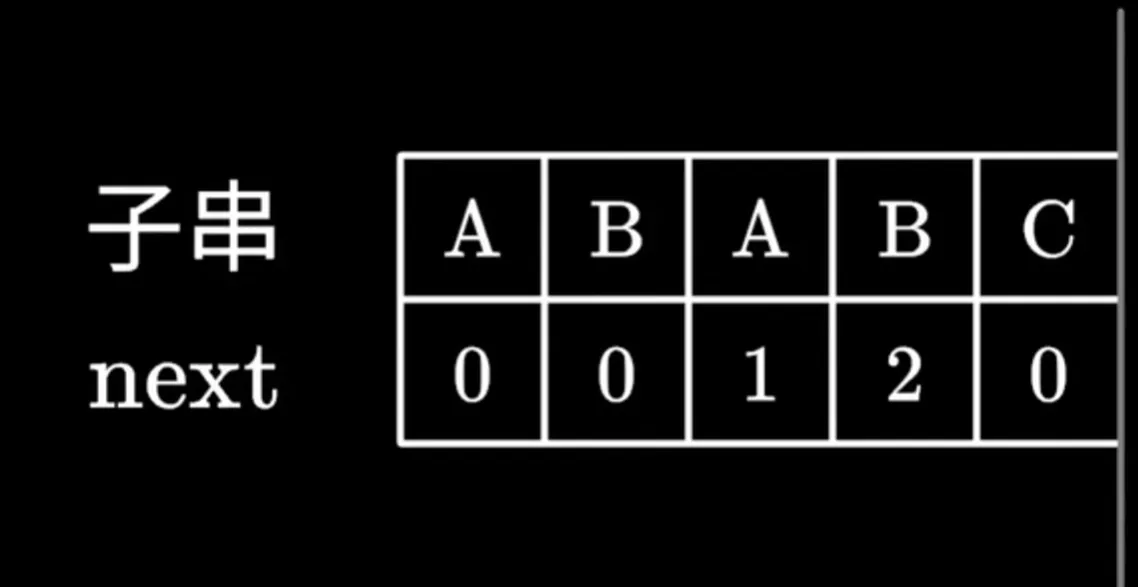
A是第一个字符没有前后缀，理所当然是0

AB很明显前后缀不相同，使用B的值记录为0

ABA可以明显发现 前面的A 和 后面的A 是一组共同前后缀且长度为1 所以当前字符A记录的值为1

ABAB 前缀为AB 后缀也为AB 所以当前字符B记录的值为2

ABABC 很明显无法找出相同的前后缀 所以当前字符C记录的值为0

接下里讲讲怎么在 O(m) 的时间复杂度内获得 next 数组。

同样需要两个指针 第一个指针指向当前共同前后缀的下一个字符（也可理解为共同前后缀的长度） 第二个指针指向最后一个元素以便判断

详细过程：

第一个字符毋庸置疑记录0 所以第二个指针是从索引1开始 第一个指针指向0

开始两指针所指元素进行比较 A 与 B 显然不同，B 也记录0，第一个指针不动，第二个指针后移

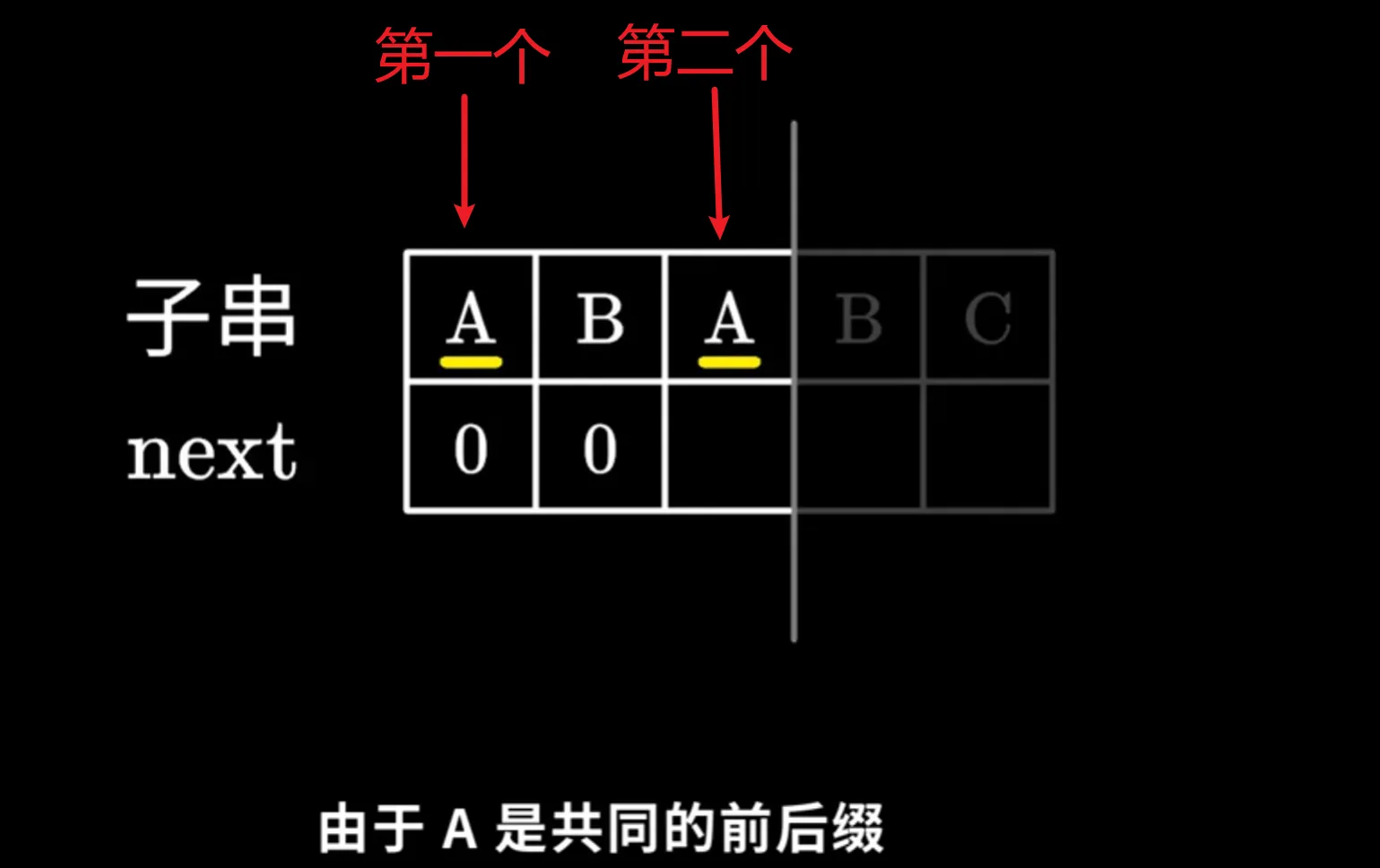
之后就是重复两个指针的比较 显然两个A可以组成一组共同前后缀长度为1 所以索引为2的A记录1 两个指针后移

显然后移后比较指针有两种情况：

• 第一种便是可以组成一个共同前后缀 指针再次后移记录值
• 第二种便是不能组成共同前后缀 这时又该怎么办呢

接下来讲讲第二种情况应该如何解决

虽然这一次比较是不同的，但是之前比较的前后缀都是相同的，我们可以把它利用起来

假如有子串ABACABAB 当比较进行到末尾的B时，与C便不同了，难道B应该记录0吗，上一次比较得到的共同前后缀是ABA

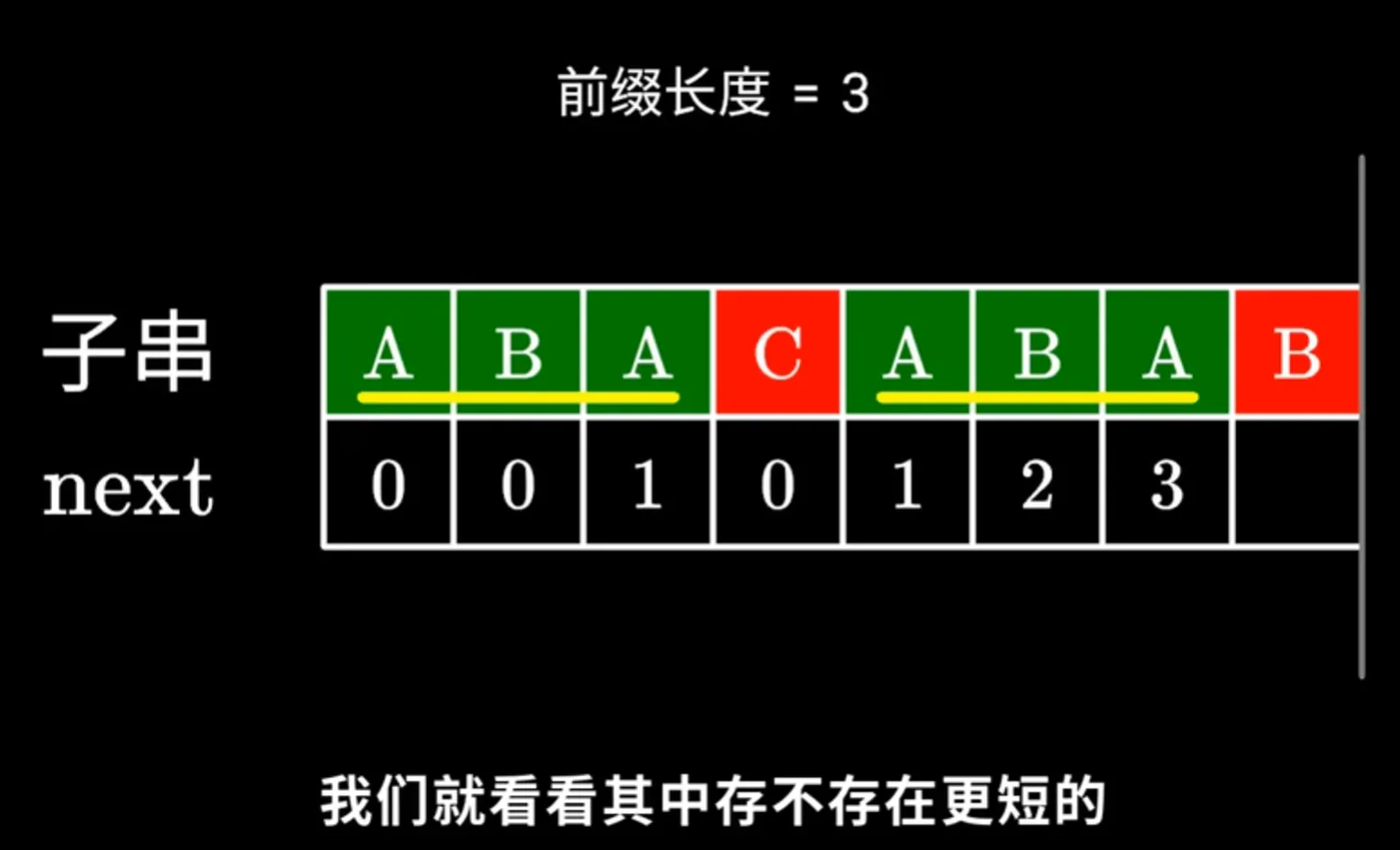
==注意接下来的内容比较难懂！！==

​ 此时我们应该考虑减少共同前后缀的长度还存不存在相同的，比如前后两个部分的ABA是完全相同，前一个ABA的前后缀与后一个ABA的前后缀相同，那么我们可以拿后一个ABA的后缀(A)(也是前一个ABA中的前缀) 去和最后一个字符B相匹配，前一个ABA中后一个A所记录的值1就是当前部分的最长共同前后缀的最大值，此时第一个指针读取它的值(也就是指针前一位所记录的值) ，也就是说只需要回退第一个指针。

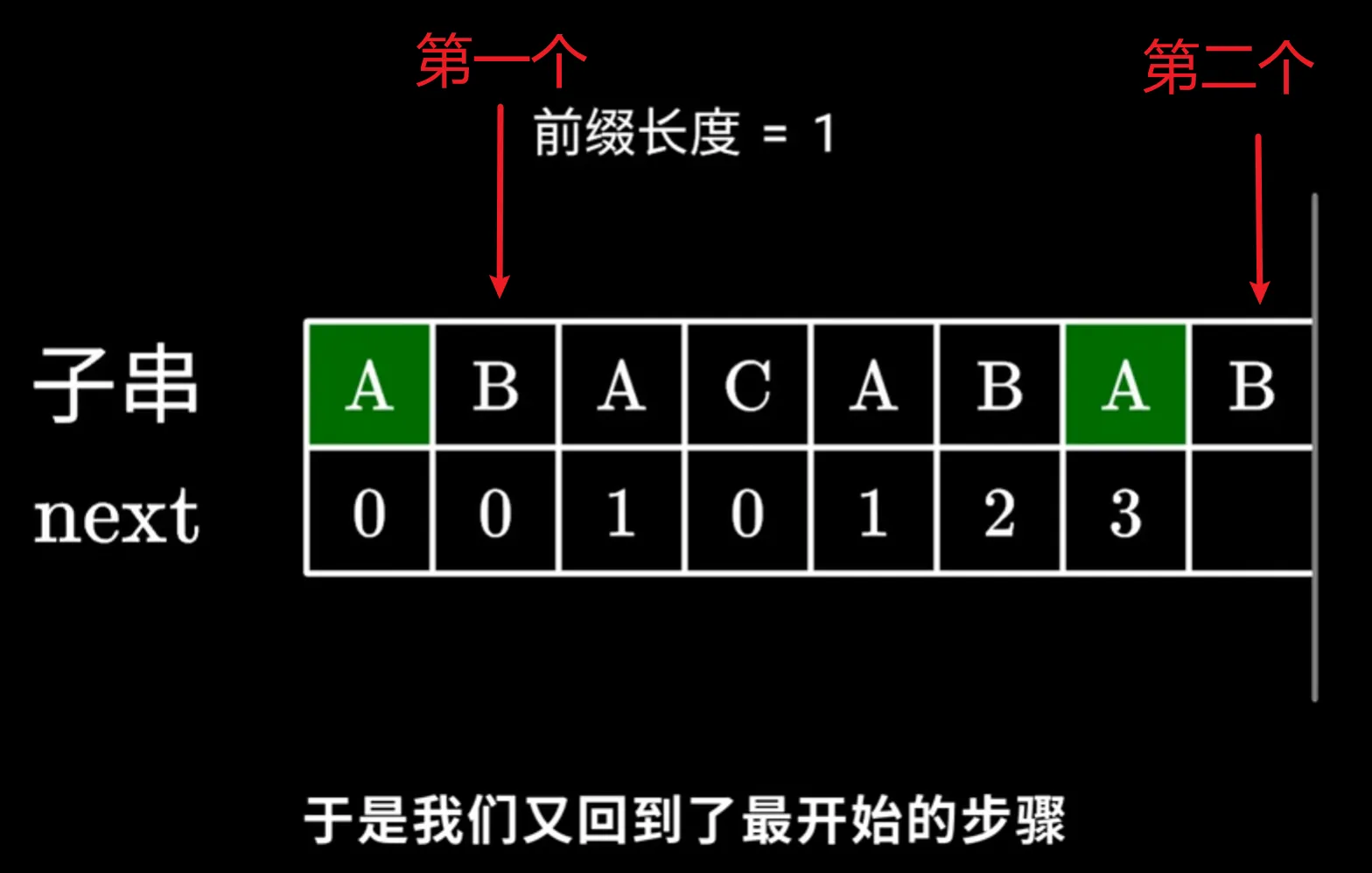
然后第一个指针指向索引为1的位置，然后再与第二个指针比较，匹配成功，所以加1，最后一个B记录2

其实这里的步骤和上面匹配时为什么读取上一个字符所记录的值的原理相同

如果不同则重复读取第一个指针前一位记录的值来移动指针 (如果值为0 则指向第一个元素)

代码实现：

int len = needle.size();
//创建next数组
vector<int> next(len);

//用递推法求next数组
int prefix_len = 0;//记录当前共同前后缀的长度(第一个指针)
	for(int i = 1;i < len2; ++i){//(i为第二个指针)
		//首先判断最后一个字母是否和前缀的后一个字母是否相同
        if(needle[prefix_len] == needle[i]){
			//相同说明可以与之前的共同前后缀组成新的共同前后缀
			prefix_len++;//移动第一个指针
            next[i] = prefix_len;//记录值
        }else{
            //不同 
            //先判断 上次共同前后缀的的长度是否为0
            if(prefix_len == 0){
              	//为0说明 最后一个字母也无法与之前的字母组成新的共同前后缀
                next[i] = 0;
            }else{
                //不为0 可以找上一次前缀部分的最长共同前后缀长度作为现在的共同前后缀长度再进行判断
                prefix_len = next[prefix_len -  1];
                i--;//保持i不变
            }
        }
	}

复杂度#

• 时间复杂度：n 为原串的长度，m 为匹配串的长度。时间复杂度为 O(m+n)。

• 空间复杂度：构建了 next 数组。时间复杂度为 O(m)。